Kinetic maturation in the germinal center

Sponsor: Amsterdam UMC

Project leaders

Prof.dr. Antoine H.C. van Kampen

Bioinformatics Laboratory, Amsterdam UMC

Dr. Marit J. van Gils

Virus vaccine immunology, Medical Microbiology, Amsterdam UMC

Dr. ir. Huub Hoefsloot

Biosystems Data Analysis, SILS, University of Amsterdam

Introduction

Systems immunology aims at understanding the immune system by combining experimental and computational methodologies to study the dynamic and non-linear interactions between its many components while focussing on clinical questions (Schmidtz, 2016; Wolkenhaur, 2013). In this project we focus on systems immunology as a novel strategy for gaining new insights in adaptive immunity in particular the germinal center (GC; Kurosaki, 2015; Victora, 2014) and, in particular, the kinetics of antibody maturation (i.e., kinetic maturation).

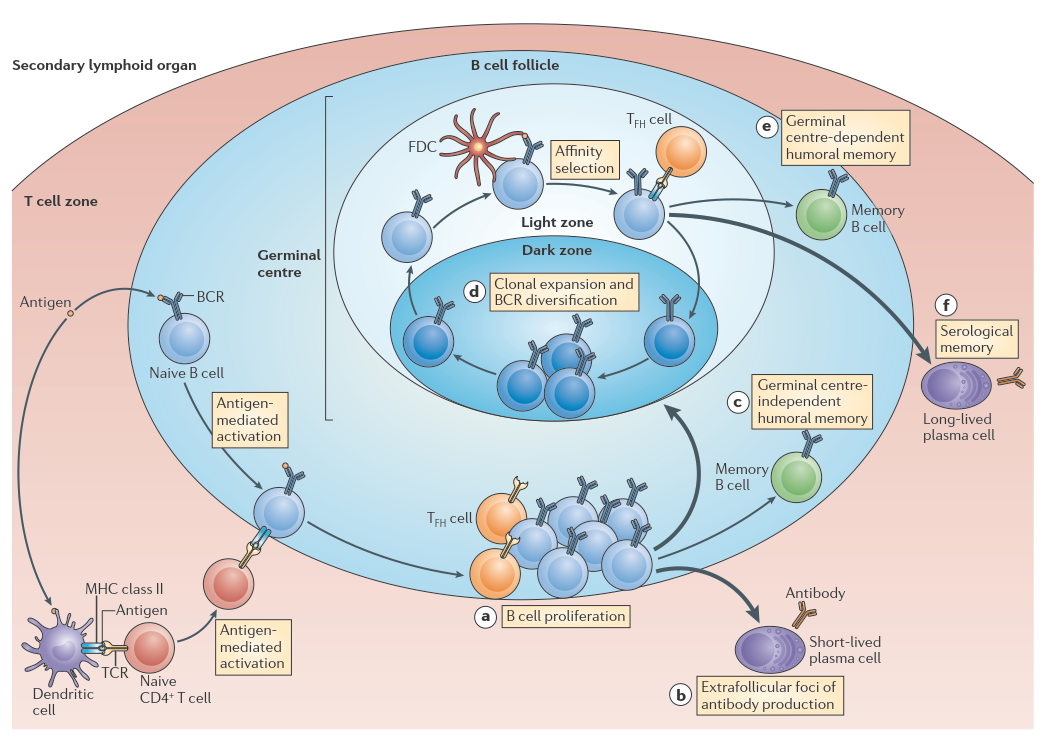
The adaptive immune system is a key component of our defence against pathogens. Its humoral component is responsible for memory B-cell formation and high-affinity antibody production (Ab) resulting from affinity maturation in germinal centres (GC; Figure 1), specialised anatomical sites typically found in secondary lymphoid tissues such as lymph nodes. B-cell clones express a unique B-cell receptor (BcR) consisting of an immunoglobulin (IG) whose variable domain is encoded by a rearrangement of the IG (V(D)J) genes. During affinity maturation, GC B cells undergo multiple rounds of proliferation, somatic hypermutation (SHM), and selection to improve their BcR affinity for the antigen. Higher affinity cells have increased probability to be positively selected for further rounds of proliferation and SHM to further diversify, or to differentiate to memory and plasma cells, hallmarks of the adaptive immunity. B cells with increased antigen-affinity are selected due to their improved capability to capture antigen from the surface of follicular dendritic cells (FDC) and to present it to a limiting number of T follicular helper cells (Tfh).

Figure 1. Germinal center reaction. Figure copied from Kurosaki (2015).

Overall aim

Development of a computational model of the GC to advance our knowledge about the role of kinetic maturation.

Method and Approach

Key-obective 1. Development of a computational model to study kinetics maturation

Agent-based models (ABM) will be used to simulate the temporal and spatial GC dynamics and outcome in different scenarios for kinetic maturation. We will extend and modify a pre-existing ABM of the GC developed by prof. dr. Michael Meyer-Hermann (Meyer-Hermann, 2012). This model implements the iterative process of affinity maturation: cell proliferation, somatic hypermutation (SHM), and positive selection of high affinity B-cells. This results in an increase of B-cell receptor (BcR) affinity and the production of high affinity plasma cells. A video of a GC simulation with the ABM was made by Danial Lashgari.

Key-objective 2. From affinity maturation to kinetic maturation

Affinity measures the strength of interaction between an epitope and a free antibody binding site. It is defined by the thermodynamic principles that govern any reversible biomolecular interaction and is inversely correlated with dissociation constant K_D that is defined as

K_D = \frac{[Ab][Ag]}{[Ab-Ag]}

and describes how much Ab-Ag complex exists at equilibrium. The time taken for this to occur depends on the kinetics of the reaction, which is determined by binding on-rate (k_{on}) and off-rate (k_{off}). That is,

K_D = \frac{1}{K_{A}} = frac{k_{off}}{k_{on}}.

Thus, instead of (only) considering GC affinity maturation one might gain further insight in the GC reaction by investigating the kinetics underlying affinity maturation, i.e., kinetic maturation. In the GC different kinetic rates may be involved in B-cell – Ag binding, and pMHC-Tfh binding. These rates can be measured by using e.g., Octet technology in vitro, and are available from published research. The upper-bound of the on-rates are constrained by mass transport (diffusion), physical reaction, and/or structural properties of the Ab and Ag. The lower-bound for off-rates may be limited by rate of endocytic uptake of Ags by B-cells. It has been shown that the off-rates correlate with neutralization of HIV and influenza virus (Klasse, 2016; Sok, 2014; Roost, 199). Because the process of affinity maturation in GCs is known to select for affinity, there seems to be no direct mechanism to select for neutralizing activity. That is, it is not known if the GC is capable of selecting for Abs with specific binding kinetics properties. In addition, different studies have shown different effects of SHM on the kinetic rates. Consequently, virtually nothing is known about possible mechanisms underlying kinetic maturation.

Currently, there seems to be no consensus about the effect of SHM on kinetic rates. Poulsen (2007) concluded that SHM is mainly improving k_{off} while k_{on} can be positively and negatively affected by SHM. Sagawa (2003) concludes that both k_{on} and k_{off} decrease during maturation. Poulsen (2011) showed that a booster vaccination improved only k_{off} while no significant changes were observed for k_{on} and K_D. Poulsen (2007) showed that there was no correlation between the number of somatic mutations and K_D, k_{on} and k_{off}, while Sagawa (2003) shows that there is a correlation between K_A and the number of mutations. Foote (1991) showed that k_{off} decreased while after booster vaccinations two groups of Abs with different k_{on} emerged. Klasse (2016) stated that affinity maturation increases the on-rates.

Kinetic maturation

Our model focuses on the kinetics of affinity maturation to gain understanding of its mechanisms and implications. The kinetic rates do not only determine B-cell and T-cell affinity but also determine the dynamics of processes involved in the GC reaction (e.g., interaction times between cells, internalization of Ag) and downstream signalling pathways (e.g., plasma cell differentiation). For example, different B-cells with the same (high) affinity but different on- and off-rates may result in different behaviour since some BcRs may be unable to stimulate signalling due to fast dissociation kinetics despite large k_{on} rates. Currently, most, if not all, GC models are based on canonical functions that change affinity (K_A) upon SHM. We will define functions that change k_{on} and/or k_{off} upon SHM to simulate and understand the kinetics of affinity maturation.

k_{on}: diffusion versus cell movement

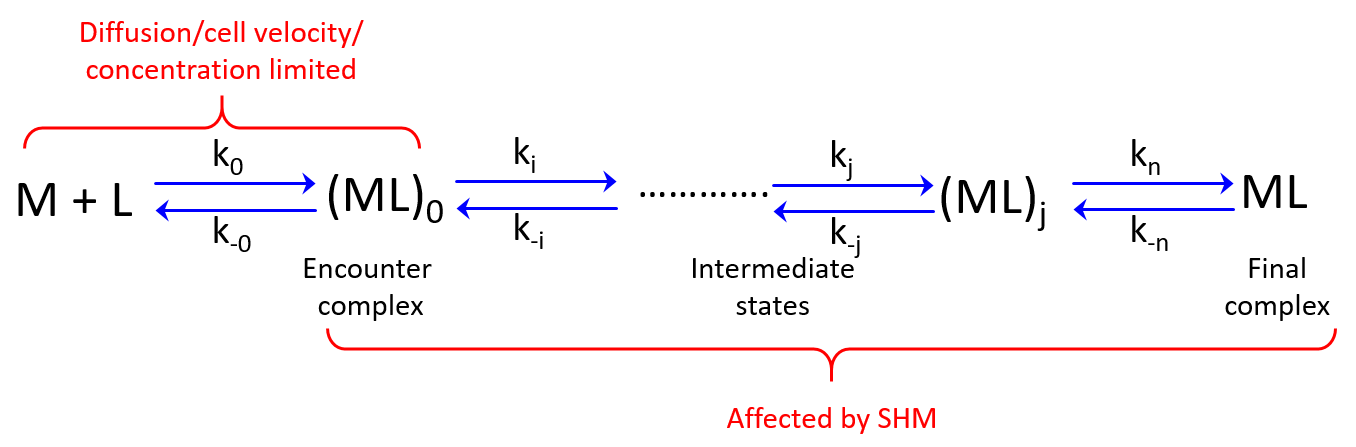
In solution k_{on} (rate to form final complex ML; Figure 2) is determined by the frequency that Ab and Ag collide. This is partially limited by diffusion (k_0 in Figure 2) if formation of the final product (ML) from the encounter complex (ML_0) is much faster than formation of the encounter complex by diffusion. Moreover, rotational diffusion effects may further decrease k_0 thereby increasing the role of diffusion (Stenberg, 1988). Hence, depending on the magnitudes of the rate constants the formation of ML may or may not be affected by the chemistry (i.e. SHM) at the Ab site (Foote, 1995).

Figure 2. Diffusion rate (k_0) and subsequent binding/conformational event rates. M = antibody, L=antigen. Rate constants are denoted by k.

This model may explain the conflicting results regarding the effect of SHM on on-rates during affinity maturation. However, the formation of complexes in solution is different from the process in the GC where we have membrane-bound Ig and the Ag is presented by FDCs or Tfh cells. Hence we do not have free diffusion of these molecules in the GC. Instead, we have cell movement that is directed by chemokine gradients. Thus, k_0 might be limited by cell velocity and concentration and unaffected by SHM if the binding reactions (k_1 to k_n) are relatively fast. Our model will be based on this and other considerations.

References

  1. Schmitz U, Wolkenhauer O, eds. 2016. Systems Medicine. New York: Springer
  2. Wolkenhauer O, Auffray C, Jaster R, Steinhoff G, Dammann O. 2013. Pediatric research 73: 502-7
  3. Kurosaki T, Kometani K, Ise W. 2015. Nat Rev Immunol 15: 149-59
  4. Meyer-Hermann M, Mohr E, Pelletier N, Zhang Y, Victora GD, Toellner KM. 2012. Cell Rep 2: 162-74
  5. Caoili SE. 2012. Adv Bioinformatics 2012: 346765
  6. Poulsen TR, Meijer PJ, Jensen A, Nielsen LS, Andersen PS. 2007. J Immunol 179: 3841-50
  7. Sagawa T, Oda M, Ishimura M, Furukawa K, Azuma T. 2003. Mol Immunol 39: 801-8
  8. Poulsen TR, Jensen A, Haurum JS, Andersen PS. 2011. J Immunol 187: 4229-35
  9. Foote J, Milstein C. 1991. Nature 352: 530-2
  10. Klasse PJ. 2016. Expert Rev Vaccines 15: 295-311
  11. Stenberg M, Nygren H. 1988. J Immunol Methods 113: 3-15
  12. Foote J, Eisen HN. 1995. Proc Natl Acad Sci U S A 92: 1254-6
  13. Tsourkas PK, Longo ML, Raychaudhuri S. 2008. Biophys J 95: 1118-25
  14. Coombs D, Kalergis AM, Nathenson SG, Wofsy C, Goldstein B. 2002. Nat Immunol 3: 926-31
  15. Tsourkas PK, Liu W, Das SC, Pierce SK, Raychaudhuri S. 2012. Cell Mol Immunol 9: 62-74
  16. Lever M, Lim HS, Kruger P, Nguyen J, Trendel N, et al. 2016. Proc Natl Acad Sci U S A 113: E6630-E8
  17. Havenar-Daughton C, Carnathan DG, Torrents de la Pena A, Pauthner M, Briney B, et al. 2016. Cell Rep 17: 2195-209